Foundation Policies with Hilbert Representations
ICML 2024
-
Seohong Park
UC Berkeley -
Tobias Kreiman
UC Berkeley -
Sergey Levine
UC Berkeley
Question
- Imagine we have a bunch of unlabeled trajectories, such as human demonstrations, task-agnostic robotic datasets, or records from previously deployed agents.
- How should we pre-train a generalist policy ("foundation policy") from such an unlabeled dataset? Which objective should we use?
- Perhaps we can use behavioral cloning (BC) or offline goal-conditioned reinforcement learning (GCRL) to pre-train policies. However, BC requires expert demonstrations and GCRL can only learn goal-conditioned policies. Is there a better way than these two?
The HILP Framework
- In this work, we propose a novel unsupervised policy pre-training scheme that captures diverse, optimal, long-horizon behaviors from unlabeled data. These behaviors are learned in a way that they can be quickly adapted to various downstream tasks in a zero-shot manner.
- Our method consists of two components: Hilbert representations and Hilbert foundation policies (HILPs).
Hilbert Representations
- Our idea starts from learning a distance-preserving representation, which we call a Hilbert representation, from offline data.
- Specifically, we train a representation \(\phi : \mathcal{S} \to \mathcal{Z}\) that maps the state space \(\mathcal{S}\) into a Hilbert space \(\mathcal{Z}\) (i.e., a metric space with a well-defined inner product) such that $$\begin{aligned} d^*(s, g) = \|\phi(s) - \phi(g)\| \end{aligned}$$ holds for every \(s, g \in \mathcal{S}\), where \(d^*\) denotes the temporal distance (i.e., the minimum number of steps).
- This can be viewed as a temporal distance-based abstraction of the state space, where temporally similar states are mapped to nearby points in the latent space. This way, we can abstract the dataset states while preserving their long-horizon global relationships.
Hilbert Foundation Policies (HILPs)
- We then train a latent-conditioned policy \(\pi(a \mid s, z)\) that spans the learned latent space with directional movements. We use the following intrinsic reward based on the inner product to train the policy: $$\begin{aligned} r(s, z, s') = \langle \phi(s') - \phi(s), z \rangle. \end{aligned}$$
- Intuitively, by learning to move in every possible direction specified by a unit vector \(z \in \mathcal{Z}\), the policy learns diverse long-horizon behaviors that optimally span the latent space as well as the state space.
- We call the resulting policy \(\pi(a \mid s, z)\) a Hilbert foundation policy (HILP) for the versatility we describe below.
Why are HILPs useful?
- HILPs have a number of appealing properties.
- First, HILPs capture a variety of diverse behaviors, or skills, from offline data. These behaviors can be hierarchically combined or fine-tuned to solve downstream tasks efficiently.
- Second, behaviors captured by HILPs are provably optimal for solving goal-reaching tasks, which makes our method subsume goal-conditioned RL as a special case, while providing for much more diverse behaviors.
- Third, the linear structure of the HILP reward enables zero-shot RL: at test time, we can immediately find the best latent vector \(z\) that solves a given task simply by linear regression.
- Fourth, the HILP framework yields a highly structured Hilbert representation \(\phi\), which enables efficient test-time planning without any additional training.
Experiments (Zero-Shot RL)
Environments
- For zero-shot RL experiments, we use four DM Control environments and ExORL datasets (Yarats et al., 2022) collected by unsupervised RL agents. Each environment provides four test tasks (e.g., Flip, Run, Stand, and Walk for Walker), where the agent must solve them at test time without any additional training.
Results
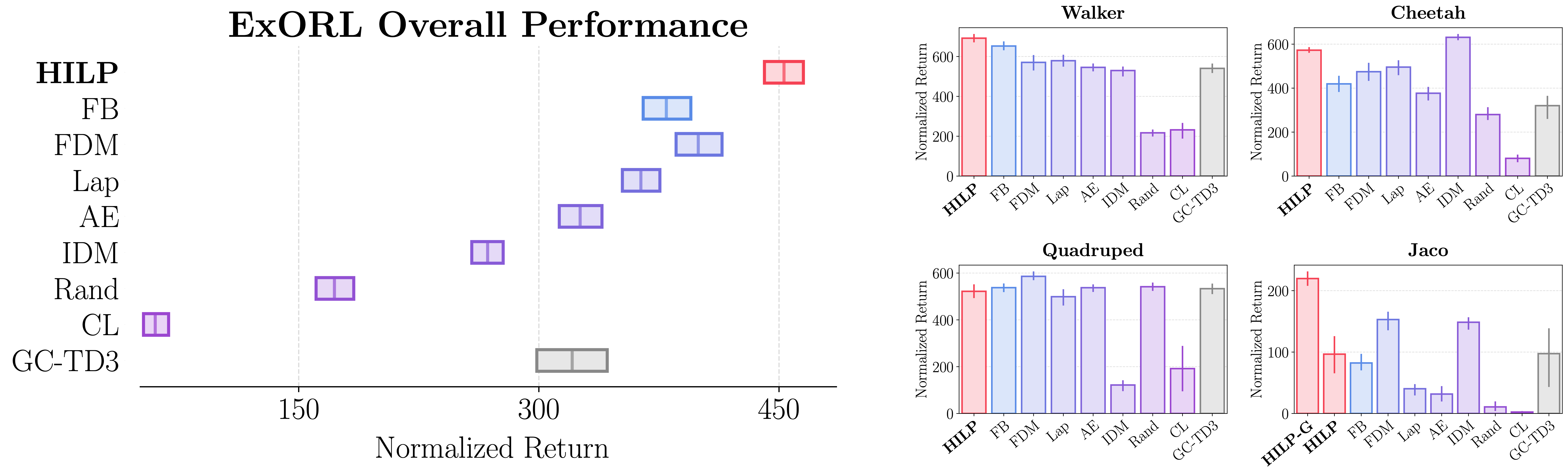
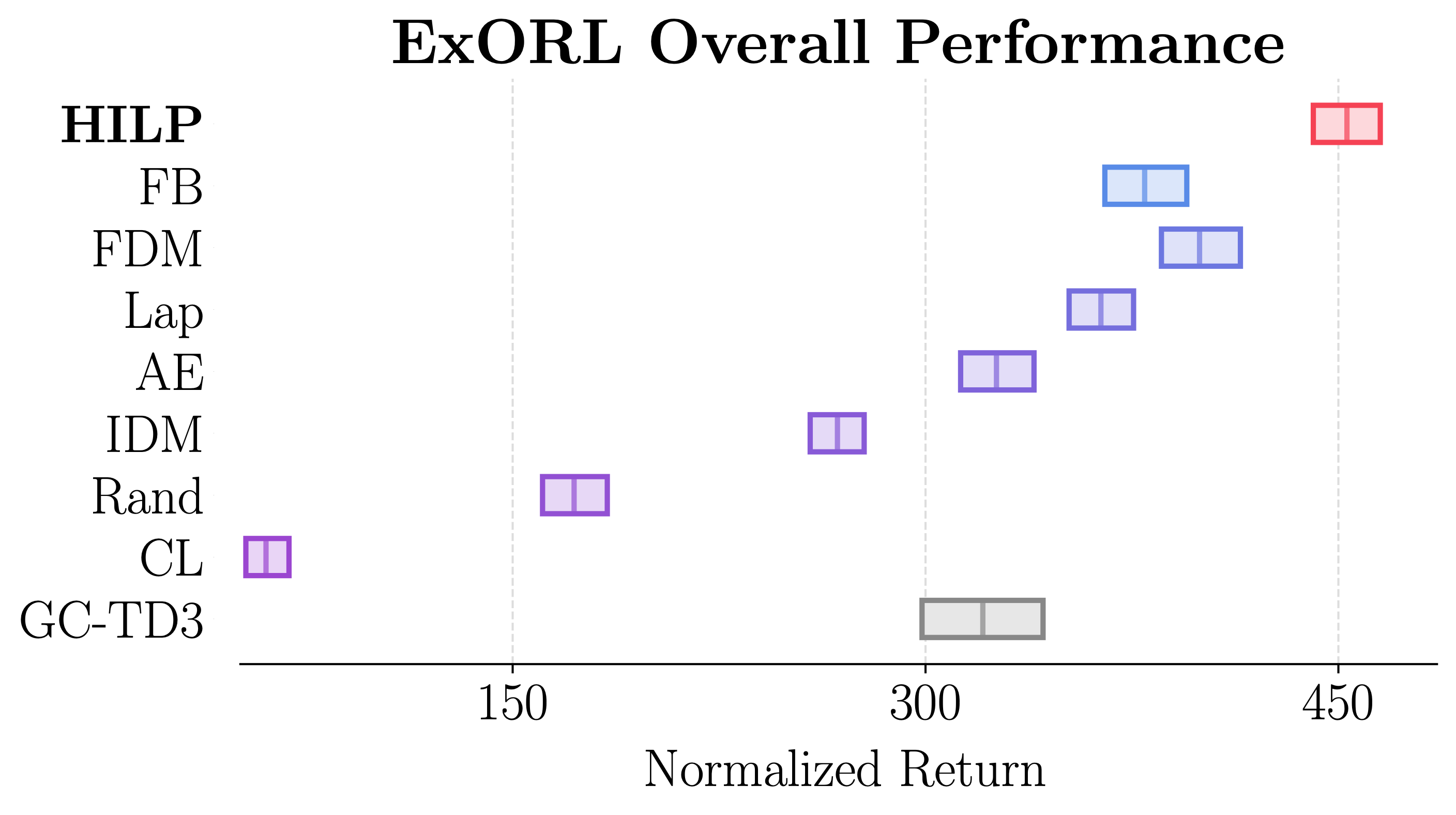
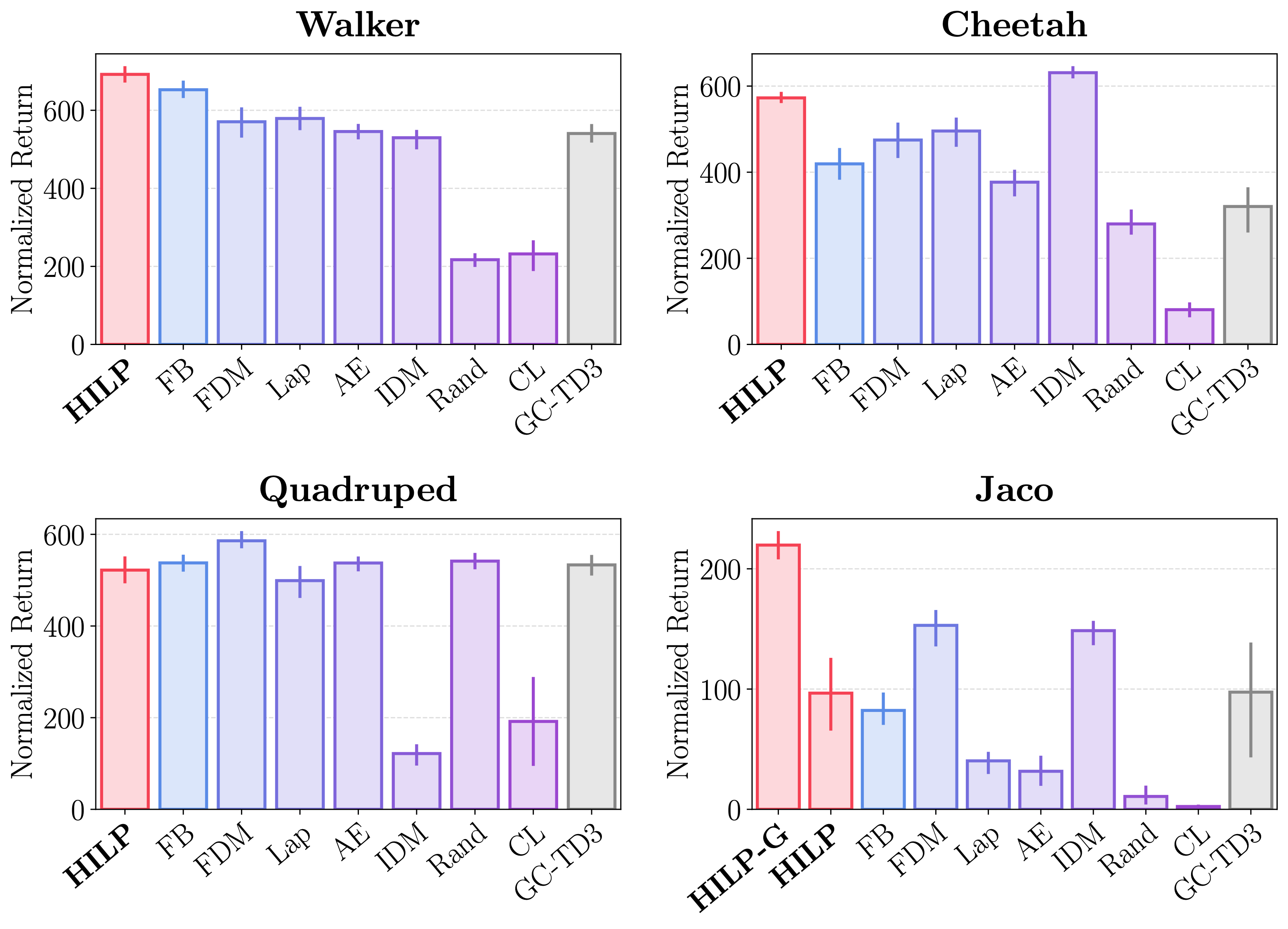
- HILPs achieve the best overall zero-shot RL performance, outperforming previous successor feature and goal-conditioned RL methods.
![]()
![]()
- Even in pixel-based ExORL benchmarks, HILPs achieve the best performance, outperforming the two strongest prior approaches.
Experiments (Offline Goal-Conditioned RL)
Environments

- For offline goal-conditioned RL, we use three challenging long-horizon environments from the D4RL benchmark suite (Fu et al., 2020). We also employ a pixel-based version of the Kitchen environment. The agent must reach a goal state from a given start state, where the goal is specified at test time.
Results
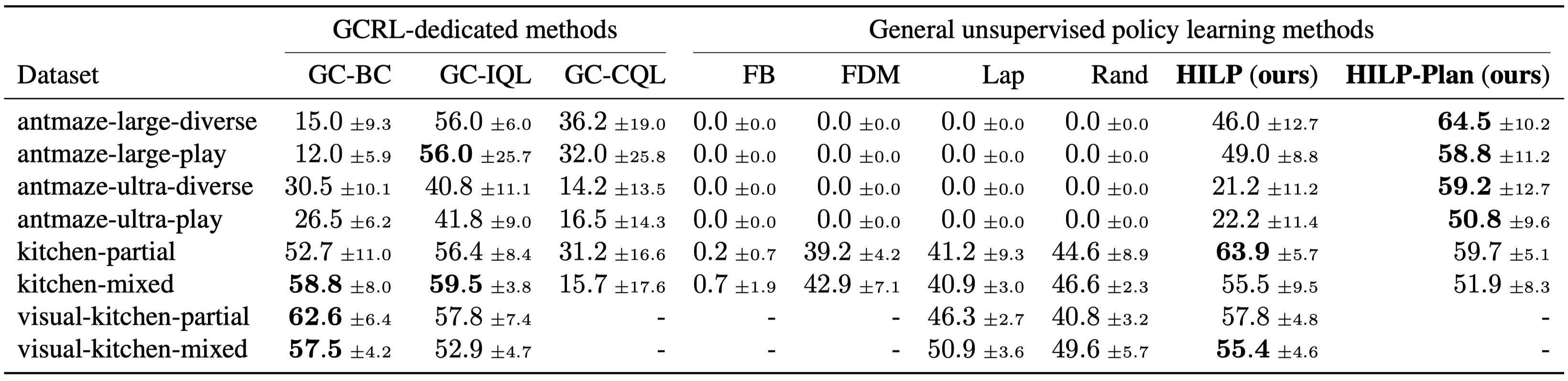
- HILPs significantly outperform previous general unsupervised policy pre-training methods, and achieves comparable performance to methods that are specifically designed for goal-conditioned RL.
- Moreover, with our efficient test-time planning procedure based on Hilbert representations, HILPs often even outperform offline goal-conditioned RL methods.
Visualization of Hilbert Representations
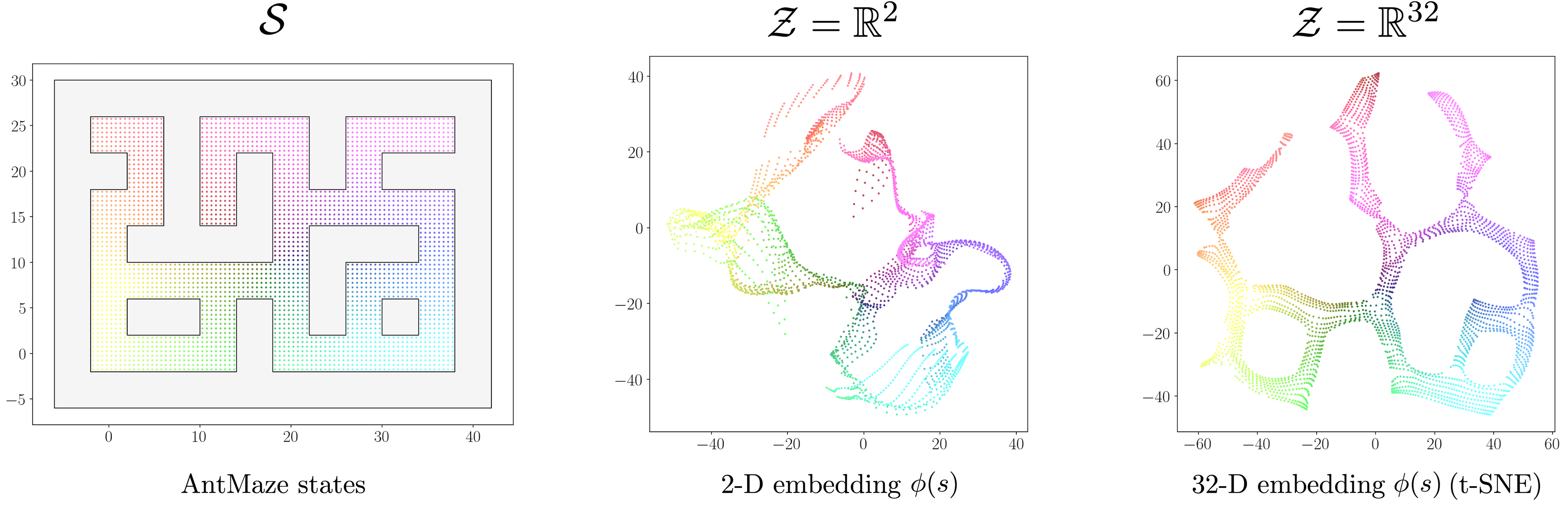
- We visualize Hilbert representations learned on the antmaze-large-diverse dataset.
- Since Hilbert representations are learned to capture the temporal structure of the MDP, they focus on the global layout of the maze even when we use a two-dimensional latent space, and accurately capture the maze layout with a 32-dimensional latent space.
- Thanks to the Hilbert structure, we can reach the goal state by simply moving in the goal direction in the latent space.
The website template was borrowed from Michaël Gharbi and Jon Barron.